differentiate

Compute the derivatives of a function along each direction. This returns a dataset with as many components as there are dimensions in the original dataset, i.e. it returns the gradient, unless the -d flag is used to specify a direction.

This command takes the basis expansion in a cell, differentiates it analytically in the desired directions, and then interpolates it onto a finer mesh in the same fashion as the interpolate command.

Note that differentiation is also possible with the ev command and the grad operation.

Command Docstrings

Command line

Command help

pgkyl differentiate -h
  Usage: pgkyl differentiate [OPTIONS]

    Interpolate a derivative of DG data on a uniform mesh

  Options:
    -b, --basistype [ms|ns|mo]  Specify DG basis
    -p, --polyorder INTEGER     Specify polynomial order
    -i, --interp INTEGER        Interpolation onto a general mesh of specified
                                amount

    -d, --direction INTEGER     Direction of the derivative (default: calculate
                                all)

    -r, --read BOOLEAN          Read from general interpolation file
    -t, --tag TEXT              Specify a 'tag' to apply to (default all tags).
    -o, --outtag TEXT           Optional tag for the resulting array
    -h, --help                  Show this message and exit.

Let’s take a gyrokinetic ion acoustic wave simulation as an example. We can examine the initial electrostatic potential generated by the initial conditions with

pgkyl gk-ionSound-1x2v-p1_phi_0.bp interp pl -x '$x$' -y '$\phi$'

giving the plot shown below on the left.

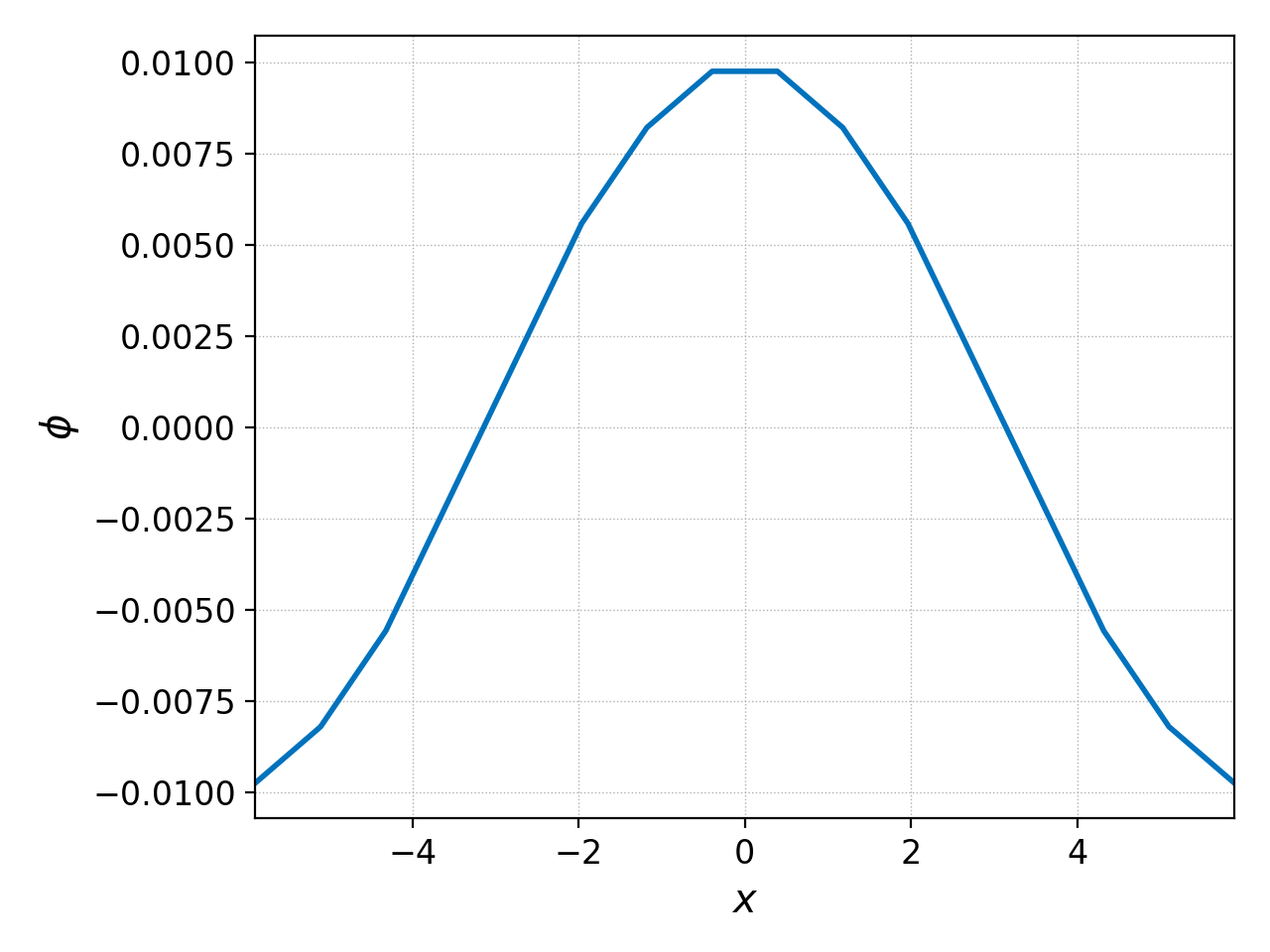
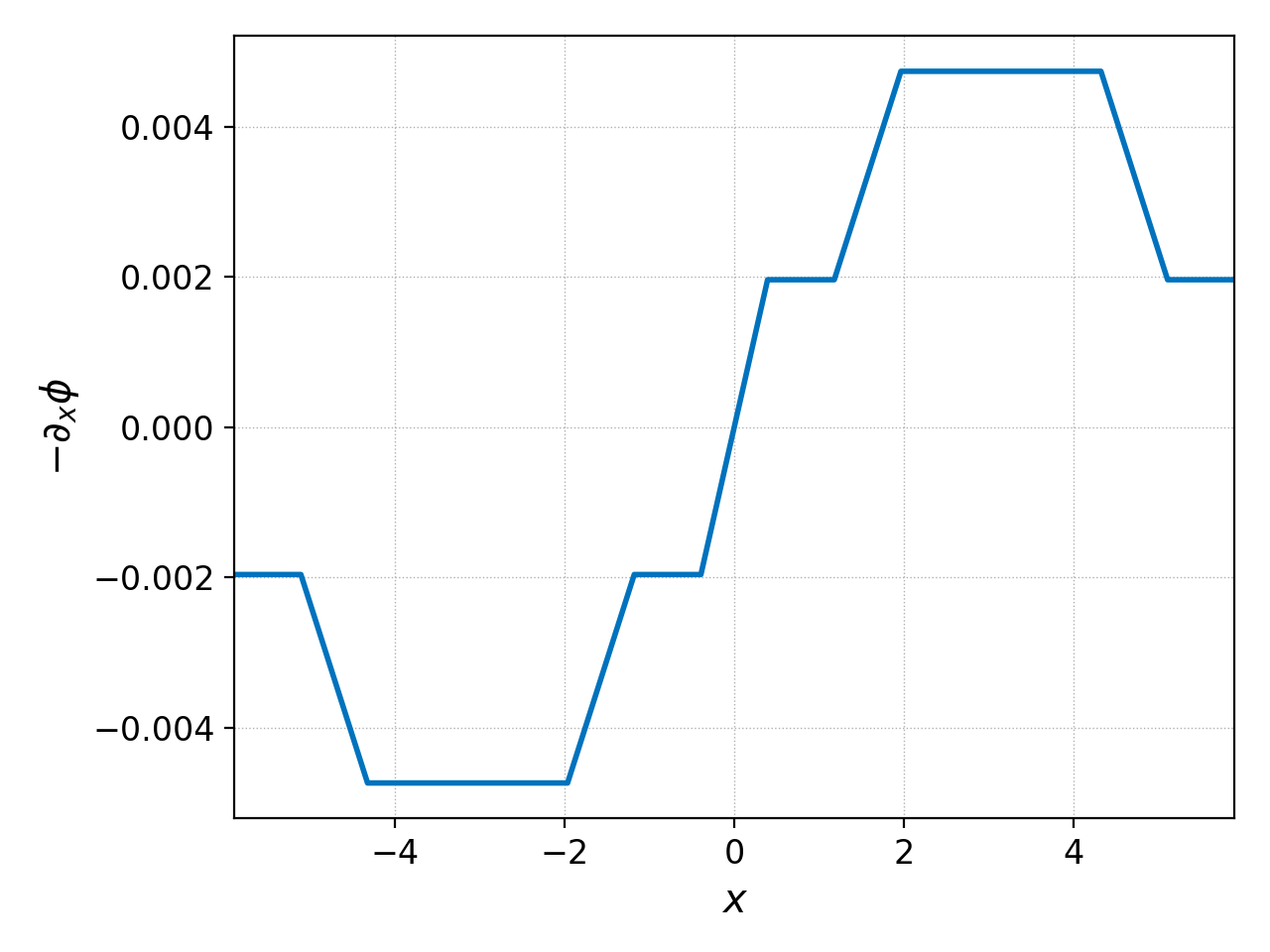
Suppose we wished to know what the initial electric field is, then we would differentiate the potential and multiply it by -1 as follows

pgkyl gk-ionSound-1x2v-p1_phi_0.bp diff -d 0 ev 'f[1] -1 *' pl -x '$x$' -y '$-\partial_x\phi$'

Note we we have abbreviated differentiate -> diff, either is allowed. This command produces the electric field above on the right. It is cellwise constant because we use a piecewise linear basis function.

Now suppose you wish to examine the gradient of the ion distribution function at \(t=0\) and \(x=0\). This can be accomplished with the following command

pgkyl gk-ionSound-1x2v-p1_ion_0.bp diff sel --z0 0. pl -x '$v_\parallel$' -y '$\mu$'

in order to produce:

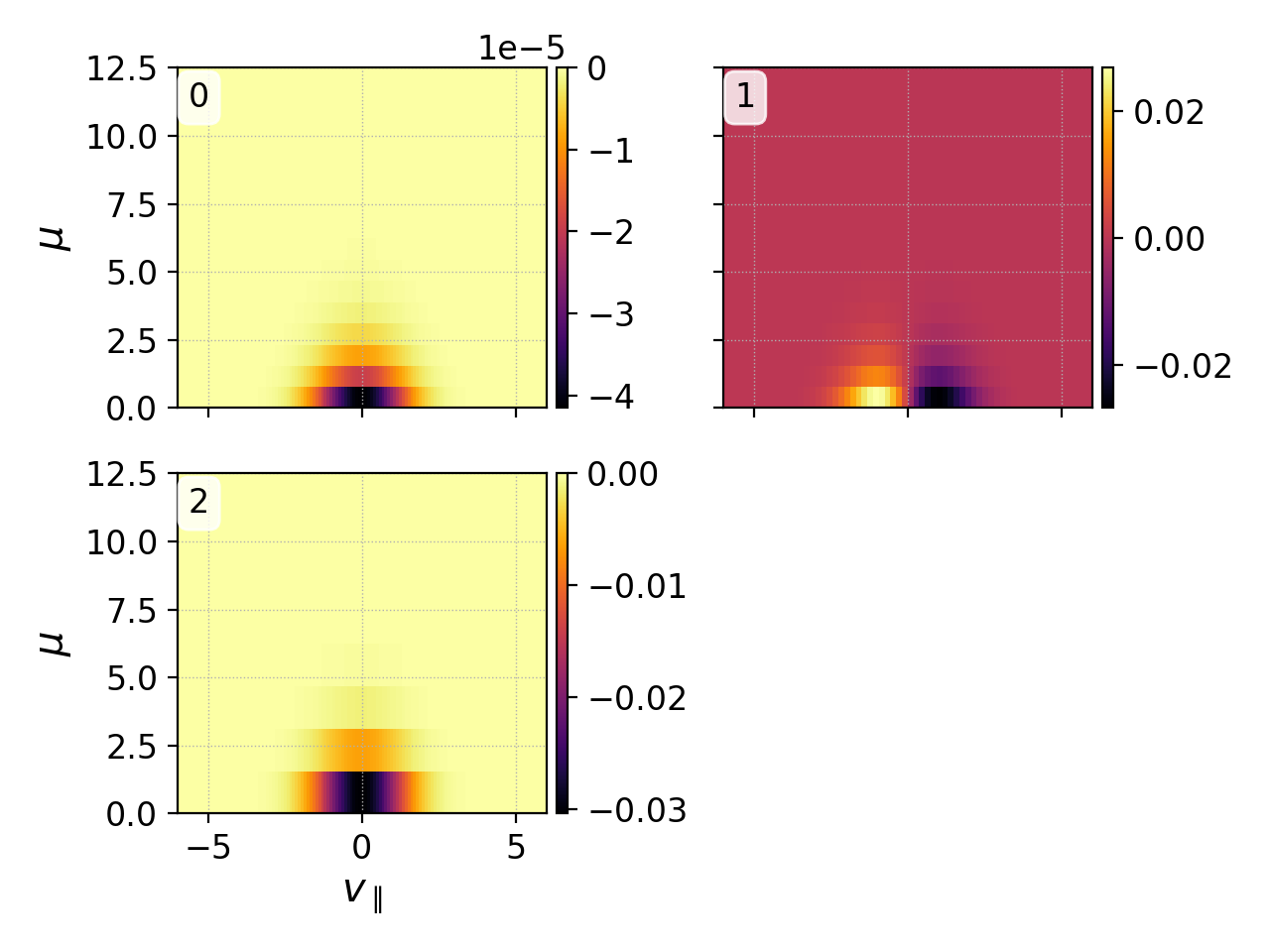
Starting with the top left and going clockwise, this plot provides the gradient in \(f_i(x,v_\parallel,\mu)\) along \(x\), \(v_\parallel\) and \(\mu\), all three evaluated at \(x=0\).